Honors Algebra 2: Assignment 48 Unit Review

Calculator Inactive.

Simplify Completely:

  1. \( \displaystyle i ^{2039}\)
    2. Solution

    \( -i\)

  2. \( \displaystyle ( 6 \mod 3) + (9 \mod 4) \)
    3. Solution

    1

  3. \( \displaystyle 3\sqrt{-10} \cdot \sqrt{-15}\)
    4. Solution

    \(-15\sqrt{6}\)

  4. \( \displaystyle \frac{\sqrt{-20}}{\sqrt{-5}}\)
    5. Solution

    2

  5. \( \displaystyle 3\sqrt{-48} + 5\sqrt{-3}\)
    6. Solution

    \( 17i\sqrt{3}\)

  6. \( \displaystyle i ^{7} + i ^{8} + i ^{9}\)
    7. Solution

    1

  7. \( \displaystyle \frac{1}{ i ^{21}} \)
    8. Solution

    \(-i\)

  8. \( \displaystyle (7 - 3 i ) - (4 + i )\)
    9. Solution

    \( 3 - 4i \)

  9. If \( \displaystyle z = 4 + 7 i\) and \(y = 2 - 3 i,\) find \(z \cdot \bar{y} \)
    10. Solution

    \( \displaystyle -13 + 26i \)

  10. \( \displaystyle \frac{1}{-3 + 2 i }\)
    11. Solution

    \( \displaystyle -\frac{3}{13} - \frac{2}{13}i \)

  11. \( \displaystyle \frac{7}{5 - i \sqrt{3}}\)
    12. Solution

    \( \displaystyle \frac{5}{4} + \frac{\sqrt{3}}{4}i \)

  12. \( \displaystyle \frac{8 - 3 i }{3 - 5 i }\)
    13. Solution

    \( \displaystyle \frac{39}{34} + \frac{31}{34}i\)

  13. Show that the conjugate of the sum of two complex numbers is the sum of the conjugates of the numbers.
    14. Solution

    Let the first number be \(a + bi\), and the second number be \(c + di\). Then the conjugate of the sum is the conjugate of \((a + c) + (b + d)i\), which is \((a + c) - (b + d)i\). The sum of the conjugates of the numbers is \(a - bi + c - di = (a + c) - (b + d)i\)

  14. Find real numbers \(x\) and \(y\) so that \( \displaystyle (x + y )i + 3x - 2 y = 7(4 + 3 i )\)
    15. Solution

    This becomes the system: \( \displaystyle \begin{align*} x + y &= 21 \\ 3x - 2y &= 28 \end{align*}. \) The solution is \( x = 14, y = 7.\)

  15. \( \displaystyle \frac{2i}{\sqrt{-16}} + i \sqrt{-27}\)
    16. Solution

    \( \displaystyle \frac{1}{2} - 3\sqrt{3} \)

Factor Completely over the complex numbers:

  1. \( \displaystyle 50x^{2} + 98\)
    2. Solution

    \( \displaystyle 2\left(5x + 7i\right)\left(5x - 7i \right) \)

  2. \( \displaystyle v^{2} + 5\)
    3. Solution

    \( \displaystyle \left(v + i\sqrt{5}\right)\left(v - i\sqrt{5}\right) \)

  3. \( \displaystyle x^{4} - y^{4}\)
    4. Solution

    \( \displaystyle (x + y)(x - y)(x + yi)(x - yi) \)

  4. \( \displaystyle x^{4} + y^{4}\)
    5. Solution

    \( \displaystyle \left( \left( x - y\frac{\sqrt{2}}{2} \right) + y\frac{\sqrt{2}}{2}i \right) \left( \left( x + y\frac{\sqrt{2}}{2} \right) - y \frac{\sqrt{2}}{2}i \right) \left( \left( x + y \frac{\sqrt{2}}{2} \right) + y\frac{\sqrt{2}}{2}i \right) \left(\left(x - y\frac{\sqrt{2}}{2}\right) - y\frac{\sqrt{2}}{2}i \right) \)

20. Solve over the complex numbers

  1. \( \displaystyle x^{2} = -121\)
    2. Solution

    \( \displaystyle x = \{ \pm 11i \} \)

  2. \( \displaystyle x - 4 - \sqrt{x - 4} = 0\)
    3. Solution

    \( \displaystyle x = \{4, 5 \} \)

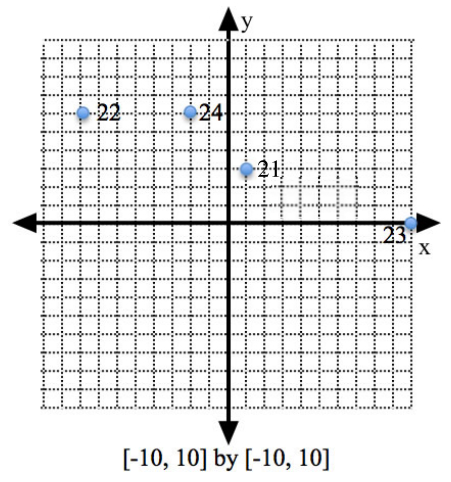
Given \(u = 1 + 3 i\), on the same set of axes, graph

  1. \( \displaystyle u\)
  2. \( \displaystyle u^{2} \)
  3. \( \displaystyle u \cdot \bar{u}\)
  4. \( \displaystyle 2u - 4\)
Solutions to #21 - #24