Simplify the following. Include domain restrictions as necessary.
- \( \displaystyle \frac{6 - x}{2x^2 - 11x - 6} \)
Solution
\( \displaystyle \frac{-1}{2x + 1}; x \neq 6 \)
- \( \displaystyle \frac{x^3 + 8x^2 - 48x}{x^2 + 11x - 60} \)
Solution
\( \displaystyle \frac{x(x + 12)}{x + 15}; x \neq 4 \)
- \( \displaystyle \frac{\displaystyle \frac{10}{a^2 - 4}}{\displaystyle\frac{6a}{a + 2} - \frac{4}{a - 2}} \)
Solution
\( \displaystyle \frac{5}{3a^2 - 8a - 4}; a \neq { \pm 2} \)
- \( \displaystyle \frac{3m}{\displaystyle \frac{m + 5}{m^2} - \frac{3}{m + 5}} \)
Solution
\( \displaystyle -\frac{3m^3(m + 5)}{2m^2 - 10m - 25}; m \neq {0, -5} \)
- \( \displaystyle \frac{\displaystyle \frac{4}{m}}{\displaystyle \frac{16}{m} - \frac{m}{4}} \)
Solution
\( \displaystyle \frac{16}{64 - m^2}; m \neq 0 \)
- \( \displaystyle \frac{\displaystyle \frac{m - 1}{m^2} - \frac{2}{m^2}}{m} \)
Solution
\( \displaystyle \frac{m - 3}{m^3} \)
- \( \displaystyle \frac{2x^2 - 5xy - 3y^2}{x^2 - 9y^2} \)
Solution
\( \displaystyle \frac{2x + y}{(x + 3y}; x \neq 3y \)
- \( \displaystyle \frac{3ac - 18ad - 2bc + 12bd}{-36a^3 + 24a^2b} \div \frac{c^2 - 36d^2}{48a^5b^2} \)
Solution
\( \displaystyle -\frac{4a^3b^2}{c + 6d}; a \neq 0, 3a \neq 2b; c \neq 6d \)
- \( \displaystyle \frac{x + 2}{3x^2 + 17x + 20} - \frac{x + 1}{9x^2 - 25} \)
Solution
\( \displaystyle \frac{2(x^2 - 2x - 7)}{(3x + 5)(3x - 5)(x + 4)} \)
- \( \displaystyle \frac {\displaystyle \frac{4x}{x^2 + 8x + 16}}{\displaystyle \frac{3}{x + 4} + \frac{2x}{\left(x + 4\right)^2}} \)
Solution
\( \displaystyle \frac{4x}{5x + 12}; x \neq -4 \)
- \( \displaystyle \frac{5x^{-1} + 9y^{-1} }{-4x^{-1} + 6y^{-1}} \)
Solution
\( \displaystyle \frac{9x + 5y}{2(3x - 2y}; x \neq 0, y \neq 0 \)
- \( \displaystyle \frac{b^{-2} - (ab)^{-1}}{\displaystyle \frac{b^{-2}}{a} - \frac{a^{-2}}{b}} \)
Solution
\( \displaystyle a; a \neq 0, b \neq 0, a \neq b \)
- \( \displaystyle c + \frac{1}{\displaystyle c + \frac{1}{c}} \)
Solution
\( \displaystyle \frac{c(c^2 +2)}{c^2 + 1}; c \neq 0 \)
- \( \displaystyle \frac{\displaystyle \frac{1}{y + 1}}{\displaystyle y - \frac{1}{\displaystyle y + \frac{1}{y}}} \)
Solution
\( \displaystyle \frac{y^2 +1}{y^3(y + 1)} \)
- \( \displaystyle \frac{\displaystyle \frac{9}{a - 7}}{1 - \displaystyle \frac{8}{a - 7}} \)
Solution
\( \displaystyle \frac{9}{a - 15}; a \neq 7 \)
- \( \displaystyle Solve: \frac{m}{m + 1} + \frac{5}{m - 1} = 1 \)
Solution
\( \displaystyle m = -\frac{3}{2} \)
- \( \displaystyle 6p^{-1} = (p - 5)^{-1} - \frac{p + 4}{p^2 - 5p} \)
Solution
\( \displaystyle p = \frac{13}{3} \)
- \( \displaystyle \frac{3}{k^2 + 5k + 6} - \frac{k - 6}{k^2 + 5k + 6} = \frac{1}{k + 3} \)
Solution
\( \displaystyle k = \frac{7}{2} \)
- The reciprocal of twice the square of the number is the reciprocal of the number minus the reciprocal of 2.
Solution
\( \displaystyle 1 \)
- \( \displaystyle \frac{1}{r + 3} = \frac{r + 4}{r - 2} + \frac{6}{r - 2} \)
Solution
\( \displaystyle r = {-8, -4} \)
- \( \displaystyle \frac{1}{k} = 5 + \frac{1}{k^2 + k} \)
Solution
\( \displaystyle k = -\frac{4}{5} \)
- \( \displaystyle \frac{x - 3}{2x + 10} + 2x - 12 = \frac{x^2 + 3x - 18}{2x + 10} \)
Solution
\( \displaystyle x = 7 \)
- The difference between the reciprocals of two consecutive positive, odd integers is the reciprocal of 7.5. Find the integers.
Solution
3 and 5
- Anabelle can complete her yard work in 3 hours. If her son helps, it will only take 2 hours. How long would the yard work take if the son was working alone?
Solution
6 h
- Norm and Cliff can paint the office in 5 hours working together. Being a professional painter, Norm can paint twice as fast as Cliff. How long would it take Cliff to paint the office by himself?
Solution
15 h
- A passanger train can travel 20mph faster than a freight train. If the passenger train can cover 390 miles in the same time it takes the freight train to cover 270 miles, how fast is each train?
Solution
Freight: 45 mph, Passenger: 65 mph
- Brett lives on the river 45 miles upstream from town. When the current is 2mph, he can row his boat downstream to town for supplies and back in 14 hours. What is his average rowing speed in still water?
Solution
7 mph
- Without a calculator, sketch the graph of \( \displaystyle y = 2 - \frac{1}{1 + x}\). Write the equations of any horizontal and vertical asymptotes.
Solution
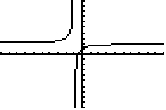Horizontal: \(y = 2\); Vertical: \(x = -1 \)- Without a calculator, sketch the graph of \( \displaystyle = \frac{1}{3 - x}\). Write the equations of any horizontal and vertical asymptotes.
Solution
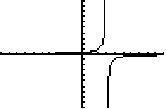Horizontal: \(y = 0\); Vertical: \(x = 3\)